Qfyilyi

Pour l'album de Stromae, voir Racine carrée (album).

Cet article ne cite pas suffisamment ses sources (mars 2008).

Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références »

En pratique : Quelles sources sont attendues ? Comment ajouter mes sources ?

La racine carrée d’un nombre réel positif x{displaystyle x} se note x{displaystyle {sqrt {x}}}.

En mathématiques élémentaires, la racine carrée d'un nombre réel positif x est l'unique réel positif qui, lorsqu'il est multiplié par lui-même, donne x, c'est-à-dire le nombre positif dont le carré vaut x. On le note √x ou x^1/2. Dans cette expression, x est appelé le radicande et le signe √ est appelé le radical^[1]. La fonction qui, à tout réel positif, associe sa racine carrée s'appelle la fonction racine carrée.

En algèbre et analyse, dans un anneau ou un corps A, on appelle racine carrée de a, tout élément de A dont le carré vaut a. Par exemple, dans le corps des complexes ℂ, on dira de i (ou de − i) qu'il est une racine carrée de − 1. Selon la nature de l'anneau, et la valeur de a, on peut trouver 0, 1, 2 ou plus de 2 racines carrées de a.

La recherche de la racine carrée d'un nombre, ou extraction de la racine carrée, donne lieu à de nombreux algorithmes. La nature de la racine carrée d'un entier naturel qui n'est pas le carré d'un entier est à l'origine de la première prise de conscience de l'existence de nombres irrationnels. La recherche de racines carrées pour des nombres négatifs a conduit à l'invention des nombres complexes.

Histoire |

Photographie de la tablette YBC 7289 avec des annotations traduisant les nombres écrits dans le système babylonien (voir l'article détaillé YBC 7289). (crédits : Bill Casselman)

La plus ancienne racine carrée connue apparaît vers 1700 av. J.-C. sur la tablette YBC 7289. Il s'agit de la représentation d'un carré avec, sur un côté, le nombre 30 et, le long de la diagonale, une valeur approchée de 2{displaystyle {sqrt {2}}}.

Construction géométrique de la racine carrée |

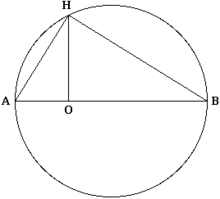
AO = 1, OB = a, OH = a{displaystyle {sqrt {a}}}

La construction géométrique suivante se réalise à la règle et au compas et permet, étant donné un segment OB de longueur a, et un segment de longueur 1, de construire un segment de longueur a{displaystyle {sqrt {a}}} :

• Construire le segment [AB] de longueur 1 + a et contenant le point O avec AO = 1


• Construire le cercle c de diamètre [AB].


• Construire la droite d perpendiculaire à (OB) et passant par O.


• Nommer H le point d’intersection du cercle c et de la droite d.

Le segment [OH] est de longueur a{displaystyle {sqrt {a}}}.

La preuve consiste à remarquer que les triangles OAH et OHB sont semblables, d'où l'on déduit que OH2=AO×OB=a{displaystyle OH^{2}=AOtimes OB=a}, et donc OH=a{displaystyle OH={sqrt {a}}}.

Cette construction a son importance dans l’étude des nombres constructibles.

Fonction réelle |

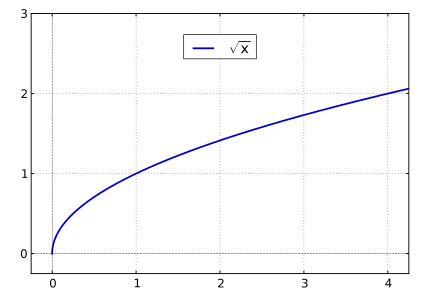
Représentation graphique de la fonction racine carrée.

L’application x↦x2{displaystyle xmapsto x^{2}} est une bijection de ℝ₊ sur ℝ₊ dont la réciproque est notée x↦x{displaystyle xmapsto {sqrt {x}}}. Cette fonction s’appelle la fonction racine carrée. Géométriquement, on peut affirmer que la racine carrée de l’aire d’un carré du plan euclidien est la longueur de l'un de ses côtés.

Mise en garde : l’aire s’exprime dans le système universel en mètres carrés et les longueurs en mètres. En prenant la racine carrée d’une quantité exprimée en mètres carrés, on obtient une quantité exprimée en mètres. Les physiciens attachent une importance particulière à l’analyse des unités ; cet aspect est effacé en mathématiques. Les nombres réels sont des constantes sans unité, et la racine carrée d’un nombre réel positif est un nombre réel positif.

La fonction racine carrée vérifie les propriétés élémentaires suivantes valables pour tous nombres réels positifs x et y :

x=x12{displaystyle {sqrt {x}}=x^{frac {1}{2}}}

x×y=x×y{displaystyle {sqrt {xtimes y}}={sqrt {x}}times {sqrt {y}}}

xy=xy{displaystyle {sqrt {frac {x}{y}}}={frac {sqrt {x}}{sqrt {y}}}} (sous la condition y>0{displaystyle y>0})

x2=|x|{displaystyle {sqrt {x^{2}}}=|x|}.

• Elle est strictement croissante, comme réciproque d'une bijection croissante sur ℝ₊.


• Elle est 1/2-höldérienne^[2] donc uniformément continue.


• Elle est dérivable en tout réel strictement positif x{displaystyle x}, mais elle n’est pas dérivable en x=0{displaystyle x=0}. En ce point, la courbe représentative admet une demi-tangente verticale. Sa fonction dérivée est donnée par :
  

  
  ddxx=12x{displaystyle {frac {mathrm {d} }{mathrm {d} x}}{sqrt {x}}={1 over 2{sqrt {x}}}}^[3].

  
  


• Elle est de classe C∞{displaystyle C^{infty }} sur ℝ₊* :∀n∈Ndndxnx=(−1)n+1(2n)!n!22n(2n−1)1xn−1/2.{displaystyle forall nin mathbb {N} quad {frac {mathrm {d} ^{n}}{mathrm {d} x^{n}}}{sqrt {x}}={(-1)}^{n+1}{(2n)! over n!2^{2n}(2n-1)}{frac {1}{x^{n-1/2}}}.}
  


• Son développement en série de Taylor au point 1 est donc, pour tout réel h tel que |h| ≤ 1 :1−h=1−∑n=1∞anhn avec an=(2n)!(n!)222n(2n−1)>0,{displaystyle {sqrt {1-h}}=1-sum _{n=1}^{infty }a_{n}h^{n}{text{ avec }}a_{n}={(2n)! over (n!)^{2}2^{2n}(2n-1)}>0,}avec convergence normale sur [–1, 1] (voir le § « Développement en série entière » de l'article « Racine d'un nombre »). Les coefficients s'expriment comme quotients de nombres de Catalan par des puissances de 2 :an=Cn−122n−1.{displaystyle a_{n}={frac {C_{n-1}}{2^{2n-1}}}.}Les premières valeurs sonta1=12,a2=18,a3=116,a4=5128.{displaystyle a_{1}={frac {1}{2}},a_{2}={frac {1}{8}},a_{3}={frac {1}{16}},a_{4}={frac {5}{128}}.}
  

Extraction de racines carrées |

Le calcul de la racine carré d'un nombre positif n'est pas toujours évident, notamment pour de grands nombres. Ainsi, plusieurs algorithmes ont été développés au cours de l'histoire afin d'obtenir ce nombre. Parmi les méthodes d'extraction de racine carrée, on peut citer notamment la méthode de Héron, qui est une méthode historique qui peut être vu d'un point de vue moderne comme un cas particulier de la méthode de Newton. D'autres méthodes sont basées sur des suites adjacentes, sur des fractions continues ou sur un principe de dichotomie.

Racines carrées particulières |

Nombre d'or |

Si p est un nombre réel strictement positif,

p+p+p+p+⋯=1+4p+12{displaystyle {sqrt {p+{sqrt {p+{sqrt {p+{sqrt {p+cdots }}}}}}}}={frac {1+{sqrt {4p+1}}}{2}}}.

Pour p = 1, on obtient le nombre d'or :

φ=1+1+1+1+⋯{displaystyle varphi ={sqrt {1+{sqrt {1+{sqrt {1+{sqrt {1+cdots }}}}}}}}}.

Nombres entiers supérieurs à 1 sous forme de racines carrées |

Ramanujan a découvert les formules suivantes :

1+21+31+…=3{displaystyle {sqrt {1+2{sqrt {1+3{sqrt {1+dots }}}}}}=3} et 6+27+38+…=4{displaystyle {sqrt {6+2{sqrt {7+3{sqrt {8+dots }}}}}}=4}.

Ces formules se généralisent, ce qui donne en particulier, pour tout réel n≥0{displaystyle ngeq 0} :

n+2=1+(n+1)1+(n+2)1+(n+3)…{displaystyle n+2={sqrt {1+(n+1){sqrt {1+(n+2){sqrt {1+(n+3){sqrt {dots }}}}}}}}} et n+3=n+5+(n+1)n+6+(n+2)n+7+…{displaystyle n+3={sqrt {n+5+(n+1){sqrt {n+6+(n+2){sqrt {n+7+dots }}}}}}}.

Pi |

Le nombre π s’exprime sous la forme d’une itération infinie de racines carrées :

π=limk→∞(2k⋅2−2+2+2+⋯2+2){displaystyle pi =lim _{kto infty }left(2^{k}cdot {sqrt {2-{sqrt {2+{sqrt {2+{sqrt {2+cdots {sqrt {2+{sqrt {2}}}}}}}}}}}}right)} , où k est le nombre de racines carrées emboitées

Ou encore :

π=limk→∞(3⋅2k−1⋅2−2+2+2+⋯2+2+3){displaystyle pi =lim _{kto infty }left(3cdot 2^{k-1}cdot {sqrt {2-{sqrt {2+{sqrt {2+{sqrt {2+cdots {sqrt {2+{sqrt {2+{sqrt {3}}}}}}}}}}}}}}right)}

(formules qui se démontrent par calcul trigonométrique direct : le terme de droite de la première, par exemple, vaut 2ksin⁡(π/2k){displaystyle 2^{k}sin(pi /2^{k})}).

Notion algébrique générale |

Définition algébrique d'une racine carrée |

Soient x et a deux éléments d’un anneau A, tels que x² = a. L'élément x est alors une racine carrée de a. La notation a{displaystyle {sqrt {a}}} est néanmoins souvent déconseillée car il peut exister plusieurs tels éléments x.

En général (si l'anneau n'est pas intègre ou s'il n'est pas commutatif), un élément peut avoir plus de deux racines carrées. Par exemple dans l'anneau Z/9Z, les racines carrées de 0 sont 0, 3 et -3, et dans le corps gauche des quaternions, tout réel strictement négatif possède une infinité de racines carrées.

Dans le cas des nombres réels, un auteur parlant d'une racine carrée de 2, traite d'un des deux éléments 2{displaystyle {sqrt {2}}} ou bien −2{displaystyle {sqrt {2}}}. En revanche, l'expression la racine carrée de deux évoque toujours la solution positive. Comme l'expression 2{displaystyle {sqrt {2}}} est toujours positive et le terme fonction racine définie sur les réels positifs désigne toujours la valeur positive, on évite cette confusion dans les enseignements un peu élémentaires des mathématiques en ne faisant usage que de l'expression : la racine carrée, alors toujours positive.

Racines carrées de nombres complexes |

La racine carrée sur ℝ est définie seulement pour les nombres positifs. Dans la résolution effective des équations polynomiales, l’introduction d’une racine carrée formelle d’un nombre négatif dans les calculs intermédiaires donne des résultats exacts. C’est ainsi que le corps des nombres complexes a été introduit^[4]

Pour tout nombre complexe non nul z=a+ib{displaystyle z=a+ib} (avec a{displaystyle a} et b{displaystyle b} réels), il existe exactement deux nombres complexes w tels que w² = z. Ils sont opposés l'un de l'autre.

• Si b est non nul, ils sont données par :

w=±(a2+b2+a2+i signe⁡(b)a2+b2−a2),{displaystyle w=pm left({sqrt {frac {{sqrt {a^{2}+b^{2}}}+a}{2}}}+i operatorname {signe} (b){sqrt {frac {{sqrt {a^{2}+b^{2}}}-a}{2}}}right),}

avec signe⁡(b)=b|b|{displaystyle operatorname {signe} (b)={frac {b}{|b|}}}.

• Si b est nul et a est négatif, cette formule se simplifie en :

w=±i|a|.{displaystyle w=pm i{sqrt {|a|}}.}

• Par ailleurs, si z n'est pas un réel négatif (i.e. si b est non nul ou si a est positif),

w=±z+|z|2(a+|z|).{displaystyle w=pm {frac {z+|z|}{sqrt {2(a+|z|)}}}.}

Pour des raisons de nature topologique, il est impossible de prolonger la fonction racine carrée, de ℝ₊ dans ℝ₊, en une fonction continue f:C→C{displaystyle scriptstyle f:mathbb {C} rightarrow mathbb {C} } vérifiant f(z)2=z{displaystyle f(z)^{2}=z}^[5].

On appelle détermination de la racine carrée sur un ouvert U de ℂ toute fonction continue f:U→C{displaystyle scriptstyle f:Urightarrow mathbb {C} } vérifiant f(z)2=z{displaystyle f(z)^{2}=z}.

La détermination principale de la racine carrée est la fonction de ℂ dans ℂ ainsi définie :
si z s’écrit sous forme trigonométrique z=reiφ{displaystyle z=re^{ivarphi }} avec −π<φ≤π{displaystyle scriptstyle -pi <varphi leq pi }, alors on pose f(z)=reiφ2{displaystyle f(z)={sqrt {r}}e^{frac {ivarphi }{2}}}. Cette détermination principale n’est continue en aucun point de la demi-droite des réels strictement négatifs, et est holomorphe sur son complémentaire.

Quand le nombre est dans sa forme algébrique z=a+ib, cette définition se traduit par :

f(a+ib)=|a+ib|+a2±i|a+ib|−a2{displaystyle f(a+ib)={sqrt {frac {left|a+ibright|+a}{2}}}pm i{sqrt {frac {left|a+ibright|-a}{2}}}}

où le signe de la partie imaginaire de la racine est

• si b≠0{displaystyle bneq 0} : le signe de b{displaystyle b}
  


• si b=0{displaystyle b=0} et a<0{displaystyle a<0} : le signe +


• si b=0{displaystyle b=0} et a≥0{displaystyle ageq 0} : pas de signe (le nombre est nul).

Notons qu’à cause de la nature discontinue de la détermination principale de la racine carrée dans le plan complexe, la relation zz′=zz′{displaystyle {sqrt {zz'}}={sqrt {z}}{sqrt {z'}}} devient fausse en général.

Racines carrées de matrices et d’opérateurs |

Si A est une matrice autoadjointe positive ou un opérateur autoadjoint positif en dimension finie, alors il existe exactement une matrice autoadjointe positive ou un opérateur autoadjoint positif B tel que B² = A. On pose alors : √A = B.

Plus généralement, pour toute matrice normale ou tout opérateur normal en dimension finie A, il existe des opérateurs normaux B tels que B² = A. Cette propriété se généralise à tout opérateur borné normal sur un espace de Hilbert.

En général, il y a plusieurs tels opérateurs B pour chaque A et la fonction racine carrée ne peut pas être définie pour les opérateurs normaux d’une façon satisfaisante (continue par exemple). Les opérateurs positifs sont apparentés à des nombres réels positifs, et les opérateurs normaux sont apparentés à des nombres complexes. Les articles sur la théorie des opérateurs développent davantage ces aspects.

Notes et références |

Voir aussi |

Articles connexes |

Lien externe |

(en) Suites concernant la racine carrée dans l'encyclopédie en ligne des suites de nombres entiers (entre autres : développements décimaux des racines carrées des entiers de 2 à 99)

Bibliographie |

• 
  (en) David Eugene Smith, History of Mathematics, vol. 2
  


• 
  (en) George Gheverghese Joseph, The Crest of the Peacock: Non-European Roots of Mathematics, 2^e éd., Penguin Books, London, 2000 (ISBN 0-691-00659-8)
  
  3^e éd. augmentée : Princeton University Press, 2010 (ISBN 978-0-691-13526-7)
  
  
  

• Portail des mathématiques