JPEG

| Extension | .jpg, .jpeg, .JPG, .JPEG |
|---|---|
| Type MIME | image/jpeg |
| Développé par | Joint Photographic Experts Group |
| Type de format | image matricielle |
| Site web | www.jpeg.org/jpeg |
JPEG (acronyme de Joint Photographic Experts Group) est une norme qui définit le format d'enregistrement et l'algorithme de décodage pour une représentation numérique compressée d'une image fixe.
Sommaire
1 Introduction au JPEG
2 Fichiers JPEG
2.1 Extensions de nom de fichiers JPEG
3 La compression JPEG
3.1 Transformation des couleurs
3.2 Sous-échantillonnage de la chrominance
3.2.1 Cas 4:4:4
3.2.2 Cas 4:2:2
3.2.3 Cas 4:2:0
3.2.4 Cas 4:1:1
3.3 Découpage en blocs
3.4 Transformée DCT
3.4.1 Remarques
3.5 Quantification
3.5.1 Remarques
3.6 Codage, compression RLE et Huffman
3.7 Décompression JPEG
3.7.1 Remarques
3.8 JPEG, codage sans pertes
4 Syntaxe et structure
5 Articles connexes
6 Notes et références
Introduction au JPEG |
JPEG est l’acronyme de Joint Photographic Experts Group. Il s'agit d'un comité d’experts qui édite des normes de compression pour l’image fixe. La norme communément appelée JPEG, de son vrai nom ISO/CEI 10918-1 UIT-T Recommendation T.81, est le résultat de l’évolution de travaux qui ont débuté dans les années 1978 à 1980 avec les premiers essais en laboratoire de compression d'images.
Le groupe JPEG qui a réuni une trentaine d’experts internationaux, a spécifié la norme en 1991. La norme officielle et définitive a été adoptée en 1992. Dans la pratique, seule la partie concernant le codage arithmétique est brevetée, et par conséquent protégée par IBM, son concepteur.
JPEG normalise uniquement l’algorithme et le format de décodage. Le processus de codage quant à lui est laissé libre à la compétition des industriels et des universitaires. La seule contrainte est que l’image produite doit pouvoir être décodée par un décodeur respectant le standard. La norme propose un jeu de fichiers de tests appelés fichiers de conformité qui permettent de vérifier qu'un décodeur respecte bien la norme. Un décodeur est dit conforme s’il est capable de décoder tous les fichiers de conformité.
Un brevet concernant la norme JPEG a été déposé par l'entreprise Forgent[1], mais a été remis en cause par le bureau américain des brevets (USPTO), qui l'a invalidé le 24 mai 2006 pour antériorité existante à la suite d'une plainte de la Public Patent Foundation[2]. Mais depuis le 27 septembre 2007, la société Global Patent Holdings, filiale d'Acacia Research Corporation, a à son tour revendiqué la paternité de ce format.
JPEG définit deux classes de processus de compression :
- avec pertes ou compression irréversible. C’est le JPEG « classique ». Il permet des taux de compression de 3 à 100[réf. nécessaire]
- sans pertes ou compression réversible. Il n’y a pas de pertes d’information et il est donc possible de revenir aux valeurs originales de l’image. Les gains en termes de compression sont alors plus modestes, avec un taux de compression de l’ordre de 2 à 8 [réf. nécessaire]. Cette partie fait l’objet d’une norme spécifique appelée JPEG-LS.
Cet algorithme est très populaire, en particulier sur Internet où la compression d'un fichier permet de réduire le coût en bande passante. Il est de plus possible d'enregistrer une image dans le format JPEG avec la majeure partie des appareils photo numériques et téléphones portables.
Cependant, les pertes se produisant lors de la compression « classique » font qu'il est moins utilisé dans certains domaines comme l'imagerie médicale, où la restitution fidèle de l'image initiale est plus importante.
Le format JPEG/JFIF supporte une taille d'image maximale de 65 535 × 65 535 pixels soit plus de quatre milliards de pixels.
Fichiers JPEG |
Extensions de nom de fichiers JPEG |
Les extensions de nom de fichiers les plus communes pour les fichiers employant la compression JPEG sont .jpg et .jpeg, cependant .jpe, .jfif et .jif furent aussi utilisées.
Il est aussi possible pour les données JPEG d'être embarquées dans d'autres types de fichiers - les fichiers codés en format TIFF contiennent souvent une image miniature JPEG de l'image principale ; et les fichiers MP3 peuvent contenir une image JPEG d'une couverture, contenue dans le tag ID3v2.
L'extension JPG est apparue dans les années 1990 parce que certains systèmes d'exploitation de cette période (ex. : Windows 95, 98, Me) ne permettaient pas d'utiliser d'extension de fichier de plus de 3 caractères.
La compression JPEG |
Le processus de compression et de décompression JPEG irréversibles comporte six étapes principales représentées ci-dessous :
 |
|---|
| Figure 1 : Organigramme de compression. |
Transformation des couleurs |
JPEG est capable de coder les couleurs sous n’importe quel format, toutefois les meilleurs taux de compression sont obtenus avec des codages de couleur de type luminance/chrominance car l’œil humain est assez sensible à la luminance (la luminosité) mais peu à la chrominance (la teinte) d'une image. Afin de pouvoir exploiter cette propriété, l'algorithme convertit l'image d'origine depuis son modèle colorimétrique initial (en général RVB) vers le modèle de type chrominance/luminance YCbCr. Dans ce modèle, Y est l'information de luminance, et Cb et Cr sont deux informations de chrominance, respectivement le bleu moins Y et le rouge moins Y.
Sous-échantillonnage de la chrominance |
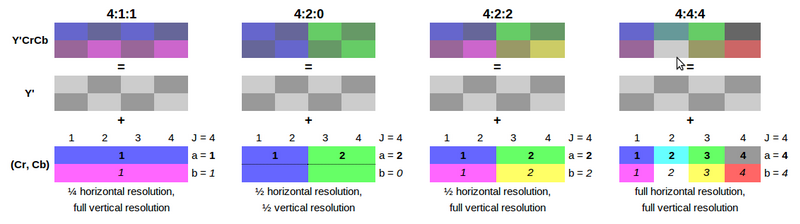
Illustration des différents types de sous-échantillonnage
Pour exploiter cette faible sensibilité de l’œil humain à la chrominance, on peut procéder à un sous-échantillonnage de ses signaux. Le principe de l'opération est de réduire de la taille de plusieurs blocs de chrominance en un seul bloc. Un traitement identique est appliqué aux blocs Cb et aux blocs Cr, tandis que les blocs de luminance (blocs Y) ne sont pas modifiés. Le sous-échantillonnage peut être réalisé selon plusieurs modes différents. Le type de mode utilisé dans une opération de compression est spécifié par la notation « J:a:b ».
L’interprétation de la notation est la suivante :
J : représente la largeur de la plus petite matrice de pixels considérée (généralement 4)
a : le nombre de composantes de chrominance dans la première ligne
b : le nombre de composantes de chrominance supplémentaires dans la deuxième ligne
Cas 4:4:4 |
Ce cas correspond à l'absence d'application du sous-échantillonnage.
Cas 4:2:2 |
Ce cas correspond à un sous-échantillonnage qui conduit à une réduction d'un facteur 1/2 de la taille des blocs Cb/Cr. Pour cela, on calcule la valeur moyenne de chrominance de deux pixels voisins horizontalement.
Cas 4:2:0 |
La moyenne de la chrominance de quatre pixels voisins est calculée et stockée dans le bloc produit par le sous-échantillonnage. Les pixels voisins forment des blocs carrés de dimension 2 × 2 pixels. Le sous-échantillonnage 4:2:0 ajoute donc une réduction verticale à la réduction horizontale du mode 4:2:2. Il conduit à une division par 4 de la taille des blocs Cb/Cr.
Cas 4:1:1 |
Ce dernier cas est rare en compression JPEG, et est plutôt appliqué dans des applications vidéo tel que les formats NTSC DV, DVCAM, DVCPRO.
Ce type de sous-échantillonnage permet de réduire de manière importante la taille des images. Cependant, il conduit à une perte d'information qui ne peut être récupérée dans la phase de décodage de l'image ; il s'agit donc d'une opération de compression irréversible. À l'issue de cette phase, les données se présentent sous la forme de blocs de coefficients Y, Cb et Cr, le nombre de blocs Cb et Cr étant égal au quart, à la moitié ou à 100 % du nombre de blocs Y selon le mode sous-échantillonnage appliqué.
Découpage en blocs |
L’image est découpée en blocs de 64 (8×8) sous-pixels. Les informations de luminance n’étant pas sous-échantillonnées, chaque bloc correspond à 8×8 pixels dans l’image d’origine. Les informations de chrominance, par contre, correspondent en fonction du sous-échantillonnage à 8×8, 16×8 ou 16×16 pixels dans l’image d’origine.
Transformée DCT |
La transformée DCT (Discrete Cosine Transform, en français transformée en cosinus discrète), est une transformation numérique qui est appliquée à chaque bloc. Cette transformée est une variante de la transformée de Fourier. Elle décompose un bloc, considéré comme une fonction numérique à deux variables, en une somme de fonctions cosinus oscillant à des fréquences différentes. Chaque bloc est ainsi décrit en une carte de fréquences et en amplitudes plutôt qu'en pixels et coefficients de couleur. La valeur d’une fréquence reflète l’importance et la rapidité d’un changement, tandis que la valeur d’une amplitude correspond à l’écart associé à chaque changement de couleur.
À chaque bloc de N⋅N{displaystyle Ncdot N}

La transformée DCT s’exprime mathématiquement par :
DCT(i,j)=2NC(i)C(j)∑x=0N−1∑y=0N−1pixel(x,y)cos[(2x+1)iπ2N]cos[(2y+1)jπ2N]{displaystyle mathrm {DCT} (i,j)={frac {2}{N}}C(i)C(j)sum _{x=0}^{N-1}sum _{y=0}^{N-1}mathrm {pixel} (x,y)cos left[{frac {(2x+1)ipi }{2N}}right]cos left[{frac {(2y+1)jpi }{2N}}right]} ![mathrm{DCT}(i, j)=frac{2}{N}C(i)C(j)sum_{x=0}^{N-1}sum_{y=0}^{N-1}<br />
mathrm{pixel}(x, y) cosleft[frac{(2x+1)ipi}{2N} right] cosleft[frac{(2y+1)jpi}{2N} right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/694b474a0ccf02a544ebf87bce6e012702450b2f) |
|---|
| Équation 1 : Transformée DCT directe. |
Et la transformée DCT inverse s’exprime par :
pixel(x,y)=2N∑i=0N−1∑j=0N−1C(i)C(j)DCT(i,j)cos[(2x+1)iπ2N]cos[(2y+1)jπ2N]{displaystyle mathrm {pixel} (x,y)={frac {2}{N}}sum _{i=0}^{N-1}sum _{j=0}^{N-1}C(i)C(j),mathrm {DCT} (i,j)cos left[{frac {(2x+1)ipi }{2N}}right]cos left[{frac {(2y+1)jpi }{2N}}right]} ![mathrm{pixel}(x, y)=frac{2}{N}sum_{i=0}^{N-1}sum_{j=0}^{N-1}<br />
C(i)C(j),mathrm{ DCT}(i, j) cosleft[frac{(2x+1)ipi}{2N} right] cosleft[frac{(2y+1)jpi}{2N} right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/1109e5107d3244f189f230922d718dd825059ceb) |
|---|
| Équation 2 : Transformée DCT inverse. |
Dans les deux cas, la constante C{displaystyle C,!}
C(x)={12pour x=01pour x>0{displaystyle C(x)=left{{begin{matrix}{frac {1}{sqrt {2}}}&mathrm {pour} ~x=0\[1ex]1&mathrm {pour} ~x>0end{matrix}}right.} ![C(x)=left{begin{matrix}frac{1}{sqrt{2}}&<br />
mathrm{pour}~ x = 0 \[1ex] 1 & mathrm{pour}~ x > 0 end{matrix}right.](https://wikimedia.org/api/rest_v1/media/math/render/svg/12acf198b1730a477b75edb7fe481673597b8948) |
|---|
| Équation 3 : Définition de la constante C. |
Pour illustrer la compression, a été repris un exemple complet provenant de Digital Image Compression Techniques de Majid Rabbani et Paul W. Jones[3].
Matrice (bloc de pixels) de base :
f=[139144149153155155155155144151153156159156156156150155160163158156156156159161162160160159159159159160161162162155155155161161161161160157157157162162161163162157157157162162161161163158158158]{displaystyle f={begin{bmatrix}139&144&149&153&155&155&155&155\144&151&153&156&159&156&156&156\150&155&160&163&158&156&156&156\159&161&162&160&160&159&159&159\159&160&161&162&162&155&155&155\161&161&161&161&160&157&157&157\162&162&161&163&162&157&157&157\162&162&161&161&163&158&158&158end{bmatrix}}}  |
|---|
| Équation 4 : Matrice d’origine. |
En effectuant la transformée DCT, on obtient la matrice des fréquences suivante :
F=[1260−1−12−52−2−31−23−17−6−3−300−1−11−9−220−1−10−7−2011000−1−1120−1112020−111−1−100−1021−1−32−4−221−10]{displaystyle F={begin{bmatrix}1260&-1&-12&-5&2&-2&-3&1\-23&-17&-6&-3&-3&0&0&-1\-11&-9&-2&2&0&-1&-1&0\-7&-2&0&1&1&0&0&0\-1&-1&1&2&0&-1&1&1\2&0&2&0&-1&1&1&-1\-1&0&0&-1&0&2&1&-1\-3&2&-4&-2&2&1&-1&0end{bmatrix}}}  |
|---|
| Équation 5 : Matrice transformée DCT. |
L'application de la DCT est une opération théoriquement sans perte d'informations ; les coefficients initiaux peuvent être retrouvés en appliquant la « DCT inverse » au résultat de la DCT. Dans la pratique, une certaine perte d'informations reste cependant possible en raison des erreurs d'arrondis introduites en cours de calcul.
Remarques |
Le calcul d’une DCT est complexe. C’est l’étape qui coûte le plus de temps et de ressources dans la compression et la décompression JPEG, mais c’est peut-être la plus importante car elle permet de séparer les basses fréquences et les hautes fréquences présentes dans l’image.
La puissance de calcul disponible aujourd’hui, alliée à des algorithmes de type FFT très efficaces, permet de rendre le temps de calcul tout à fait acceptable pour l’utilisateur courant, voire imperceptible avec les machines les plus puissantes.
À la suite de cette étape, les basses et hautes fréquences sont distinguées. Les basses fréquences constituent les données majeures présentes dans une image, les hautes fréquences, quant à elles, caractérisent les zones à fort contraste, qui sont les changements brusques de couleur. Ces données étant moins visibles, c'est donc sur celles-ci que la compression s'effectuera.
Quantification |
La quantification est l’étape de l'algorithme de compression JPEG au cours de laquelle se produit la majeure partie de la perte d'information (et donc de la qualité visuelle), mais c'est aussi celle qui permet de gagner le plus de place (contrairement à la DCT, qui ne compresse pas).
La DCT a retourné, pour chaque bloc, une matrice de 8×8 nombres (dans l’hypothèse que les blocs de l’image font 8×8 pixels). La quantification consiste à diviser cette matrice par une autre, appelée matrice de quantification, et qui contient 8×8 coefficients spécifiquement choisis par le codeur.
Le but est ici d’atténuer les hautes fréquences, c’est-à-dire celles auxquelles l’œil humain est très peu sensible. Ces fréquences ont des amplitudes faibles, et elles sont encore plus atténuées par la quantification ; certains coefficients sont même souvent ramenés à 0.
Le calcul permettant la quantification est le suivant :
F∗(u,v)=⌊F(u,v)+⌊Q(u,v)2⌋Q(u,v)⌋≅{displaystyle F^{*}(u,v)=leftlfloor {F(u,v)+leftlfloor {Q(u,v) over 2}rightrfloor over Q(u,v)}rightrfloor cong }  entier le plus proche (F(u,v)Q(u,v)){displaystyle left({F(u,v) over Q(u,v)}right)} entier le plus proche (F(u,v)Q(u,v)){displaystyle left({F(u,v) over Q(u,v)}right)} |
|---|
Avec : ⌊x⌋{displaystyle lfloor xrfloor } entier directement inférieur à x{displaystyle x,!} entier directement inférieur à x{displaystyle x,!} |
| Équation 6 : Calcul de la quantification. |
Et pour la quantification inverse :
F^(u,v)=F∗(u,v)⋅Q(u,v){displaystyle {hat {F}}(u,v)=F^{*}(u,v)cdot Q(u,v)}  |
|---|
| Équation 7 : Calcul de la quantification inverse. |
Comme le montre l'exemple ci-dessous, la quantification ramène beaucoup de coefficients à 0 (surtout en bas à droite dans la matrice, là où se trouvent les hautes fréquences). Seules quelques informations essentielles (concentrées dans le coin en haut à gauche) sont gardées pour représenter le bloc. La redondance des données contenues dans le bloc augmente ainsi fortement, ce qui peut être exploité par un algorithme de compression : au moment de coder le résultat dans le fichier, la longue suite de zéros nécessitera très peu de place. Cependant, si la quantification est trop forte (= taux de compression trop élevé), il y aura trop peu de coefficients non nuls pour représenter fidèlement le bloc. Le problème apparaîtra lors du décodage nécessaire pour l'affichage de l'image : à l’écran la division en blocs deviendra visible, et l'image aura un aspect « pixellisé ».
Dans notre exemple, nous avons pris la matrice de quantification suivante :
Q=[1611101624405161121214192658605514131624405769561417222951878062182237566810910377243555648110411392496478871031211201017292959811210010399]{displaystyle Q={begin{bmatrix}16&11&10&16&24&40&51&61\12&12&14&19&26&58&60&55\14&13&16&24&40&57&69&56\14&17&22&29&51&87&80&62\18&22&37&56&68&109&103&77\24&35&55&64&81&104&113&92\49&64&78&87&103&121&120&101\72&92&95&98&112&100&103&99end{bmatrix}}}  |
|---|
| Équation 8 : Matrice définissant le niveau de quantification. |
Ce qui donne comme matrice des fréquences quantifiée :
F∗=[790−1 0 0 0 0 0 −2−1000000−1−10000000000000000000000000000000000000000000000]{displaystyle F^{*}={begin{bmatrix}79&0&-1&~0~&~0~&~0~&~0~&~0~\-2&-1&0&0&0&0&0&0\-1&-1&0&0&0&0&0&0\0&0&0&0&0&0&0&0\0&0&0&0&0&0&0&0\0&0&0&0&0&0&0&0\0&0&0&0&0&0&0&0\0&0&0&0&0&0&0&0end{bmatrix}}}  |
|---|
| Équation 9 : Matrice quantifiée. |
Remarques |
Codage, compression RLE et Huffman |
Le codage s’effectue en zigzag comme le montre la figure suivante et se termine par un caractère de fin :
 |
|---|
| Figure 2 : Ordre de codage défini par la norme JPEG. |
Codage de notre exemple : 79,0,−2,−1,−1,−1,0,0,−1,EOB{displaystyle 79,0,-2,-1,-1,-1,0,0,-1,EOB,!}
Ce résultat est ensuite compressé selon un algorithme RLE basé sur la valeur 0 (le codage RLE intervient uniquement sur cette dernière), puis un codage entropique de type Huffman ou arithmétique.
Avec le schéma de codage très simplifié suivant, on remarque que le codage nous délivre deux tables (quatre pour une image couleur). Ces tables étant enregistrées dans le fichier final peuvent être choisies par le compresseur.
 |
|---|
| Figure 3 : Schéma de codage simplifié. |
Décompression JPEG |
Les étapes de la décompression s’effectuent dans l’ordre inverse de la compression suivant les méthodes définies précédemment (en même temps que la compression).
Voici dans notre exemple le résultat de la décompression :
f=[144146149152154156156156148150152154156156156156155156157158158157156155160161161162161159157155163163164164162160158156163163164164162160158157160161162162162161159158158159161161162161159158]{displaystyle f={begin{bmatrix}144&146&149&152&154&156&156&156\148&150&152&154&156&156&156&156\155&156&157&158&158&157&156&155\160&161&161&162&161&159&157&155\163&163&164&164&162&160&158&156\163&163&164&164&162&160&158&157\160&161&162&162&162&161&159&158\158&159&161&161&162&161&159&158end{bmatrix}}}  |
|---|
| Équation 10 : Résultat de la décompression. |
Ainsi que la matrice d’erreur :
e=[−5−2011−1−1−1−41123000−5−1350−101−101−2−1024−101−2−1024−2−2−3−3−2−3−1021−110−4−2−143001−3−10]{displaystyle e={begin{bmatrix}-5&-2&0&1&1&-1&-1&-1\-4&1&1&2&3&0&0&0\-5&-1&3&5&0&-1&0&1\-1&0&1&-2&-1&0&2&4\-1&0&1&-2&-1&0&2&4\-2&-2&-3&-3&-2&-3&-1&0\2&1&-1&1&0&-4&-2&-1\4&3&0&0&1&-3&-1&0end{bmatrix}}}  |
|---|
| Équation 11 : Matrice des erreurs réalisées par les pertes. |
Remarques |
Les erreurs sont au maximum de 5 et en moyenne 1,6 sur environ 150 ce qui nous donne une erreur moyenne d’environ 1 %, et tout cela pour un passage de 64 à 10 valeurs (avec le caractère de fin) ; à cela, il faut rajouter la matrice de quantification, mais comme généralement on compresse de gros fichiers, elle n’influence que peu.
JPEG, codage sans pertes |
Ici, la précision p des échantillons varie de 2 à 16 bits. À la place de la DCT, le codage utilise un prédicteur P à trois échantillons.
 |
|---|
| Figure 4 : Schéma de compression JPEG sans pertes. |
Syntaxe et structure |
JPEG peut désigner soit le codage d'une image, soit le format de fichier. En effet, différents formats de fichiers (TIFF, PDF, JPG…) peuvent contenir une image codée en JPEG. On parlera dans ce paragraphe du format de fichier (aussi appelé JFIF pour JPEG File Interchange Format).
Un fichier JPEG est constitué d'une séquence de segments commençant par un marqueur. Un marqueur se compose de la valeur 0xFF suivie d'un octet identifiant le type de marqueur. Certains marqueurs ne contiennent que ces deux octets ; d'autres sont suivis de deux octets spécifiant la taille en octets des données du segment. Cette taille inclut ces deux octets de taille mais pas ceux du marqueur.
| Abréviation | Valeur | Contenu | Nom | Commentaires |
|---|---|---|---|---|
| SOI | 0xFFD8 | aucun | Start Of Image | Premiers octets du fichier |
| SOF0 | 0xFFC0 | taille variable | Start Of Frame (Baseline DCT) | Indique une image codée par baseline DCT, et spécifie la largeur, la hauteur, le nombre de composantes et le sous-échantillonnage des composantes (par exemple 4:2:0). |
| SOF2 | 0xFFC2 | taille variable | Start Of Frame (Progressive DCT) | Indique une image codée par progressive DCT, et spécifie la largeur, la hauteur, le nombre de composantes et le sous-échantillonnage des composantes (par exemple 4:2:0). |
| DHT | 0xFFC4 | taille variable | Define Huffman Table(s) | Spécifie une ou plusieurs tables d'Huffman. |
| DQT | 0xFFDB | taille variable | Define Quantization Table(s) | Spécifie une ou plusieurs tables de quantification. |
| DRI | 0xFFDD | deux octets | Define Restart Interval | Spécifie l'intervalle entre les marqueurs RSTn, en macroblocs. Ce marqueur est suivi de deux octets indiquant sa taille de sorte qu'il puisse être traité comme n'importe quel segment de taille variable. |
| SOS | 0xFFDA | taille variable | Start Of Scan | Commence un parcours de haut en bas de l'image. Dans les codages baseline DCT, il n'y a généralement qu'un seul parcours. Les images progressive DCT contiennent habituellement plusieurs parcours. Ce marqueur spécifie quelle tranche de données il contient. La taille n'est pas indiquée : il est immédiatement suivi par des données codées entropiquement. Les octets 0xFF sont suivis par un octet 0x00 pour ne pas être confondus avec des marqueurs. |
| RSTn | 0xFFD0 … 0xFFD7 | aucun | Restart | Insère tous les r macroblocs, où r est l'intervalle DRI (cf. marqueur DRI). Il n'est pas utilisé s'il n'y a pas de marqueur DRI. Les trois bits de poids faible du code de marqueur varient en boucle de 0 à 7. |
| APPn | 0xFFEn | taille variable | Application-specific | Ce marqueur permet d'inclure des informations qu'un programme de visualisation peut ignorer tout en restant capable de décoder l'image. Par exemple, un fichier JPEG Exif utilise un marqueur APP1 pour enregistrer des métadonnées, organisées selon une structure proche du formatage TIFF. |
| COM | 0xFFFE | taille variable | Commentaire | Contient un commentaire textuel. |
| EOI | 0xFFD9 | aucun | End Of Image | Derniers octets du fichier |
Articles connexes |
- DCT
- Compression d'image
Notes et références |
(en) Site de Asure Software - nouveau nom de Forgent depuis 2007
(en)« Patent Asserted Against JPEG Standard Rejected by Patent Office as Result of PUBPAT Request », sur pubpat.org, 26 mai 2006(consulté le 3 avril 2012)
(en) Majid Rabbani et Paul W Jones, Digital Image Compression Techniques, Bellingham, Spie Optical Engineering Press, 1991, 240 p. (ISBN 0819406481, OCLC 23142891)
« ISO/IEC 10918-1 : 1993(E) p.36 »
- Portail de l’imagerie numérique